9 Bisection

Having spent quite a while investigating linear systems of equations, we now turn to the nonlinear world. Systems of nonlinear equations look difficult, so we will start by looking for ways to estimate the roots of single variable functions.

Our first method is one we encountered during the calculus review. Recall the intermediate value theorem and its proof.

Theorem 9.1 Let \(f:\mathbb{R}\to \mathbb{R}\) be continuous on \([a, b]\) and assume \(f(a)\) and \(f(b)\) have different signs. Then, \(f\) must have a root in \([a, b]\).

Proof. We inductively define sequences \(a_k,b_k,c_k\) in \([a,b]\) such that \(f(a_k)\) and \(f(b_k)\) have different signs, and \(c_k = \frac{a_k + b_k}{2}\). We start from \(a_0=a\) and \(b_0=b\).

Then consider \(f(c_k)\). If it is zero, we’ve found a root and can stop. Otherwise, it has a sign. Since \(f(a_k)\) and \(f(b_k)\) have different signs, and there are only two signs, \(f(c_k)\) must disagree with one of them. If it’s \(a_k\), we set \(a_{k+1} = a_k\) and \(b_{k+1} = c_k\). If \(b_k\), we do the opposite.

By construction, the \(a_k\) and \(b_k\) sequences are monotonic (increasing and decreasing, respectively) and certainly bounded, so their limits exist. Moreover, since the replacement is by the average, the distance halves at each step, \[b_k - a_k = \frac{b-a}{2^k},\] so the limits coincide. Let \(c\) be the limit. The construction ensures that \(f\) takes both positive and negative values in every open interval containing \(c\). However, if \(f\) were continuous and \(f(c) \neq 0\) then for a sufficiently small interval around \(c\), the sign of \(f\) would always match the sign of \(f(c)\).

This method is quite easy to implement. At each step, we only need to keep the most recent \(a_k\) and \(b_k\) values, so it does not take much space either.

def bisection(f,a,b,n):
    if f(a)*f(b) > 0:
1        raise ValueError('f(a) and f(b) must have different signs')
    if a > b: # accomodates backward intervals
        a,b = b,a
    for i in range(0,n):
        c = (a+b)/2
2        if f(c) == 0:
            return c
        elif f(a)*f(c) > 0:
            a = c
        else:
            b = c
    return c

1: We can’t check continuity, of course.
2: In practice, this is very unlikely, and one could reasonably drop it to save a little time. See the related programming exercise.

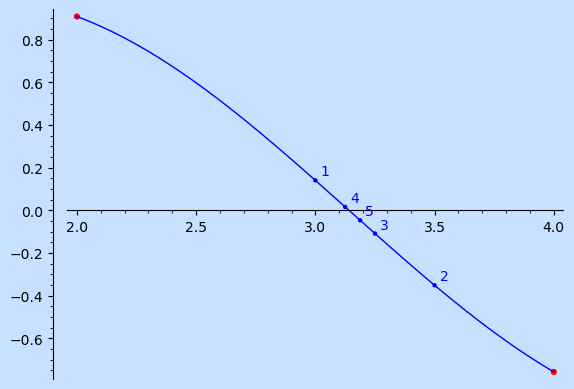
We can use this to estimate \(\pi\) as a root of \(\sin(x)\) in the interval \([2,4]\).

\(\displaystyle \frac{1609}{512} \approx 3.142578125\)

\(\displaystyle \frac{3294199}{1048576} \approx 3.1415929794311523\)

You may notice that the accuracy isn’t great. The estimate \(c_n\) is at most \[\frac{b-a}{2^{n+1}}\] from a root because \(c_n\) is the midpoint of an interval of length \((b-a)/2^n\) containing a root. That means 20 steps only guarantees us 5 or 6 (decimal) digits.

We can visualize the steps.

Exercises

Exercise 9.1 There are functions which aren’t continuous but still satisfy the statement of the intermediate value theorem: for all \(a,b\) in their domain and \(y\) between \(f(a)\) and \(f(b)\), there is some \(x\) between \(a\) and \(b\) such that \(f(x) = y\). These functions are said to have the intermediate value property.

For example, the derivative of any function has the intermediate value property, but need not be continuous.

Although the IVT is true for these functions, the bisection method can still fail. Find an example of a function with the IVP and an interval \([a,b]\) such that the bisection method does not find a root of the function.

Programming Problems

Exercise 9.2 Computer representations of numbers typically can’t identify zero, nor accurately carry out calculations in a way that guarantees the signs are correct. This is a subtle issue, so we consider handling a simplified case. Suppose we have a (small) tolerance \(t\) such that our computer’s calculations for this problem are always accurate to an error of at most \(t\). In other words, if \(|x| < t\), we cannot be sure whether or not \(x\) is zero, but if \(|x| > t\) then we know that \(x\neq 0\).

Implement a modified bisection method which, incorporates the tolerance: test whether \(|f(c)| < t\) rather than \(f(c) = 0\), and check the signs of \(f(a)\) and \(f(c)\) separately rather than the shortcut \(f(a)f(c) > 0\). It should also end if \(b-a < t\), since that means the estimates are not changing with further steps, from the perspective of the computer.

Write one version which runs a specified number of steps, and another version which runs until finding \(c\) such that \(|f(c)| < t\) (or is otherwise forced to exit) and reports the number of steps this took.